Melanie Schmidt

Algorithms and Data Structures group
Dr. Anja Rey
Lukas Drexler
Julian Wargalla
Annika Hennes
Laura-Marie Hagemann

Alumni
Giulia Baldini
Vincent Gramlich

Heinrich-Heine-Universität Düsseldorf
Universitätsstraße 1
40225 Düsseldorf

mschmidt@hhu.de

DBLP Google Scholar

Theoretical analysis of practically important aspects of cluster analysis

Heiko Röglin
Melanie Schmidt
Anna Arutyunova
Julian Wargalla

The area of cluster analysis is concerned with the search for unknown structure in data. The goal is to find hidden clusters, i.e., groups of points that belong together. Clustering has many applications in the area of data analysis and has thus been studied in various variations, leading to a huge body of clustering research.
However, clustering also suffers from a large gap between theory and practice, even with respect to the objective functions that are studied. In theory, combinatorial problems like k-center and k-median are extremely well studied.

   

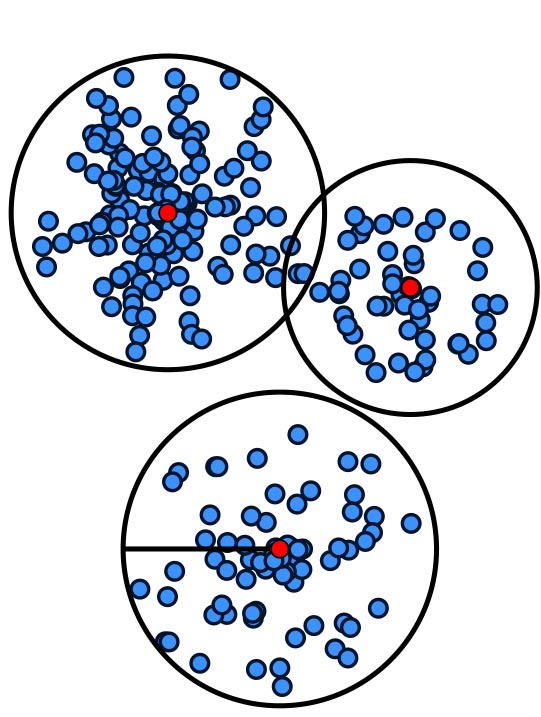
In practice, methods for very different types of problems play a much larger role, e.g., for k-means clustering or for hierarchical clustering. Additionally, there can be additional demands on the solution, leading to constrained clustering problems. Our goal is the theoretical analysis of practically relevant questions in the area of cluster analysis. This includes the study of the approximability of more practical variants of clustering as well as the analysis of popular heuristics, e.g., under structural assumptions on the input data. Our project consists of two parts.

Clustering with constraints (Melanie Schmidt)

In the first part, we consider the effect of constraints on clustering problems. Examples for constraints are capacities, lower bounds, fairness constraints and outliers. First, we want to develop better approximation algorithms for clustering problems with constraints. Second, we want to analyze popular heuristics and develop practically efficient algorithms. In both cases, we are also interested in combining different constraints. Third, we want to study clustering problems with constraints in data streams.

Hierarchical clustering (Heiko Röglin)

The second part considers hierarchical clustering. Instead of fixing a specific number of clusters k, hierarchical clustering computes a hierarchy of clusterings. Hierarchical clusterings play a major role in applications, yet they have been studied very little in theory. First, we want to analyze the approximation ratio of the very popular greedy heuristics for hierarchical clustering. Second, we want to develop approximation algorithms with small approximation ratios, which are not yet known for most of the variants of hierarchical clustering. We are also interested in lower bounds on the ratios of algorithms and lower bounds on the approximability itself. Third, we want to develop global objective functions for hierarchical clustering.

Approximation Algorithms for Geometric Data Analysis and Their Practicability

We are looking for a PostDoc to cooperate with this project! See here.

Geometric data analysis is an emerging field on the intersection of computational geometry and machine learning that is concerned with the analysis of data that has geometric properties. Algorithmic data analysis is a term that is being established for designing methods for data analysis by using techniques from the areas of algorithms, theory or algorithm engineering. In this project we are interested in algorithmic geometric data analysis, or, more precisely, in approximation algorithms for geometric data analysis tasks. The focus is on finding algorithms with provable performance guarantees, and on translating them into methods that are practically efficient from the view point of algorithm engineering.

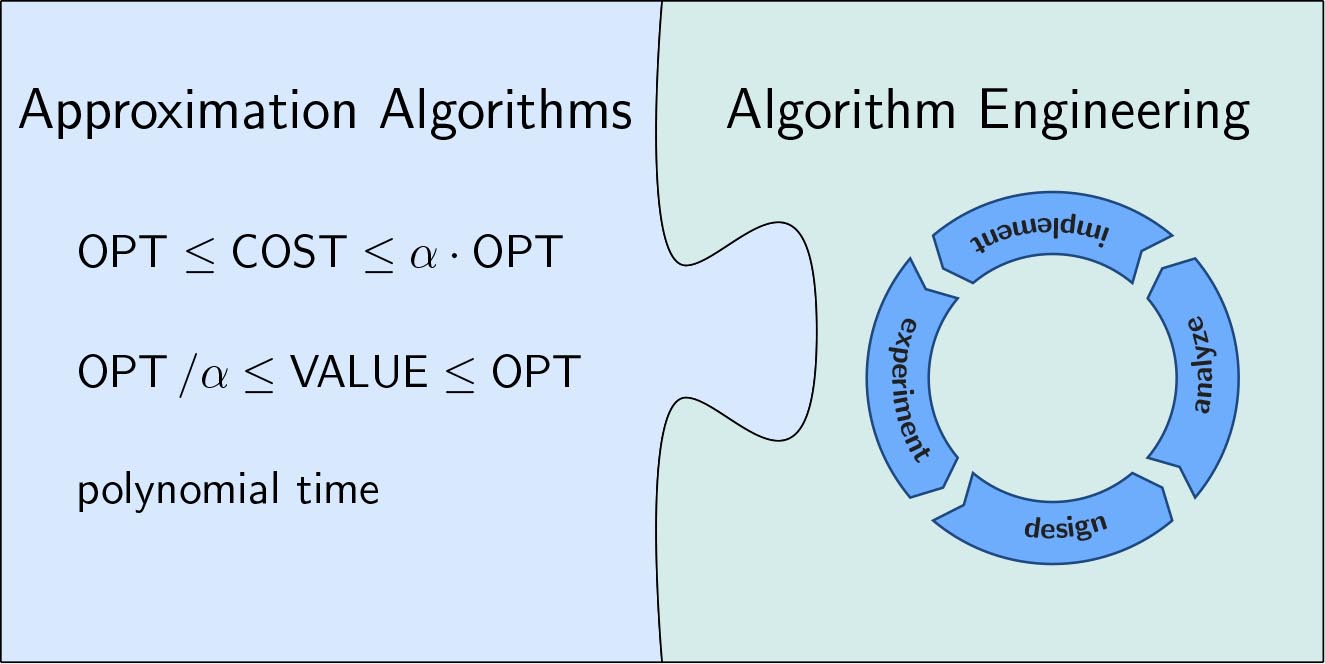
Data analysis tasks are often very difficult to solve, involve side constraints or have a complicated combinatorial structure. Approximation algorithms run in polynomial time and provide a provable bound on the worst quality produced. They are particularly interesting for solving data analysis tasks in practice if they are also practically efficient and provide high quality results (often much better than their theoretical guarantee). The area of practical approximation algorithms for data analysis tasks has gained a lot of popularity lately. We will pursue this approach for different geometric data analysis tasks with a focus on clustering and in particular k-means.